
来源: 职业数学家在民间
天上有多少颗星星,数学中就有多少个未解之谜。如果要我从数学中选出一颗最神秘的星星,那我一定会选著名的 3n+1 猜想。
看似非常简单的一个问题
3n+1 猜想的具体表述是非常简单的:
对任何正整数n做如下变换,如果 n 是偶数,则让它变成n/2(也就是减半); 如果 n 是奇数,则让它变成 3n+1。任何一个正整数n,一直按照这个法则变换下去,最终会变成1。
下面是几个简单的例子:
1、从 12 开始,我们得到变换序列 12, 6, 3, 10, 5, 16, 8, 4, 2, 1。
2、从 19 开始,我们得到变换序列 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1。
3、从 27 开始,情况变得复杂了,按照上面的法则,变换的整数值逐渐变大,最大值达到 9232,不过最终还是变回1:
27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1
目前,人们对于小于 1018 的数都已经验证了 3n+1 猜想。
但验证和证明完全是两码事。
就是这样一个连小学生都能听懂的猜想,它的证明难倒了这个时代的所有数学家!
所有!
数学还没有成熟到足以解决这样的问题
现在已经无法确切考证 3n+1 猜想到底是谁先提出来的。但是有文献显示早在上个世纪 30 年代,德国数学家 Lothar Collatz 就考虑过类似问题,所以 3n+1 猜想经常被称作考拉茨(Collatz)猜想。由于 3n+1 猜想是由一个名叫角谷的日本人传到中国,所以在国内又称角谷猜想。当然了它还有许多其他的名字,但我认为称其为 3n+1 猜想是最合适的。

Lothar Collatz(1910-1990)
上个世纪五六十年代,3n+1 猜想传入美国后,疯狂吸引了大量的数学专业师生,据说这个猜想传入耶鲁大学数学系时,整个系的人,从本科生到资深教授,在整整一个月的时间内都在试图证明它。同样的事情也发生在芝加哥大学。当时甚至有人宣称,3n+1 猜想可能是一个试图摧毁美国数学研究事业的阴谋。
时至今日,关于 3n+1 猜想的研究也不是没有进展,比较有代表性的工作是 Krasikov 和 Lagarias 在 03 年发表在《Acta Arithmetica》的论文中证明的结果:
在比 n 小的整数中,能满足这个猜想的整数的个数至少是 cn0.84 。其中c是一个固定常数。
但这些工作和 3n+1 猜想本身比起来太微弱了,丝毫没有撼动这个巨石猜想。
3n+1 猜想到底有多难呢?大数学家厄特希(P.Erdos)曾说过:“数学还没有成熟到足以解决这样的问题!” 数学天才陶哲轩也认为这个猜想不太可能被当前的技术证明。
背后是一大堆的猜想和问题
3n+1 猜想并非一个孤立的猜想,而是一大堆类似猜想中最简单,最有代表性的一个例子。3n+1 猜想本身也可以有许多的延拓和推广。
注意所有的整数可以分成偶数(2n 型)和奇数(2n+1 型)这两类。如果我们定义如下的正整数函数 f ,它在偶数和奇数上分别定义为:
f(2n)=n; f(2n+1)=3(2n+1)+1,
那么 3n+1 猜想等价于说任何正整数在f的迭代下都会进入循环4→2→1。
如果把f扩充为所有整数的函数,那么广义的 3n+1 猜想是说任何整数在f的迭代下都会进入下面四个循环

当然,我们也可以把 3n+1 替换成 3n+m,(其中m是任意不被 3 整除的奇数)。那么 3n+m 猜想是说任何整数在相关函数的迭代下都会进入有限个循环。
但是,如果我们用把 3n+1 替换成 kn+1(k是大于 3 的奇数),那么新函数的迭代性质就有了根本的变化,我们一般都猜想,当k大于 3 时,几乎所有整数在新函数的迭代下会趋于无穷。所有这些猜想的难度都绝不亚于 3n+1 猜想本身。
最后再举另外一个比较著名的整数迭代函数 U 。注意所有的整数可以分成偶数(2n 型),4n+1 型的数和 4n+3 型的数,这三类,而U函数在这三类数上的定义分别为:
U(2n)=3n; U(4n+1)=3n+1; U(4n+3)=3n+2。
这个迭代函数也是由考拉茨(Collatz)最先考虑过的。Murray Klamkin 在 1963 年提出一个公开的问题:
整数n=8 在函数U的迭代下是否趋于无穷?
一般我们都认为应该会趋于无穷,比如迭代序列刚开始时是:
8→12→18→27(27=4*6+3)→20→30→45(45=4*11+1)→34→51→38→57→……
但这样一个如此特殊的猜想到现在也依然无法证明。
太难太难了!
而这仅仅是我们在这一大类问题里所碰到的最为简单,最为特殊的情形。关于这一类问题的最一般的表述和猜想,以及 3n+1 猜想的历史,大家可以参考 Lagarias 编辑的论文专著《The Ultimate Challenge: The 3x+1 Problem》。这部专著取名:《终极挑战》。
是啊,3n+1 猜想当之无愧地成为对人类智力的终极挑战!
和现有的数学分支有多少关联呢?
如果从 1 出发,运用逆向的变换法则,我们就会得到著名的考拉茨图(Collatz graph),下面是 19 步逆向变换内得到的考拉茨图
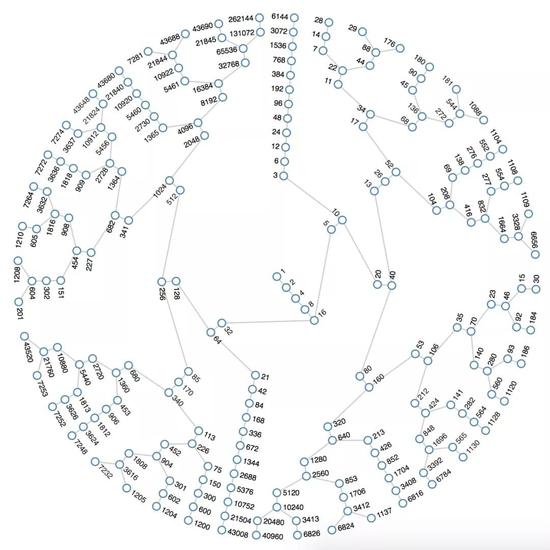
围绕考拉茨图(Collatz graph),从图论的角度,有许许多多很有意思的研究工作,但基本上都无助于解决 3n+1 猜想。
另外,3n+1 猜想中修正的迭代函数
f(2n)=n; f(2n+1)=(3(2n+1)+1)/2=3n+2
也可以扩充成2-adic 整数环,或者复数域上的迭代函数,因此可以从遍历理论或者复动力系统的角度来研究 3n+1 猜想。特别值得一提的是复数域上的迭代函数 F 有如下比较简单的表达形式:
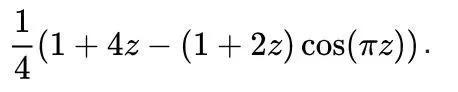
下面是这个函数 F 的 Julia 集,也就是在 F 的迭代下保存有界的那些复数构成的集合。是不是很美?其实许多函数的 Julia 集都非常精美!

值得一提的是在 1972 年, 数学家 Conway 证明了 3n+1 猜想比较一般的推广问题从数理逻辑的角度来看是不可判定的(undecidable)。但这也无助于解决 3n+1 猜想和其他具体的类似猜想,就像所有丢番图方程不可判定的著名结论无助于求解具体的丢番图方程。
还有一些工作从概率论和随机过程的角度理解 3n+1 猜想,或者将其与有限维代数联系起来,并得出一些等价命题,限于篇幅我们就不一一介绍了,有兴趣的朋友可以查阅这两本专著。

遥远而又神秘的未知世界透射过来的一缕微光
其实数学各个领域中都不乏著名的难题和猜想,比如黎曼猜想,多项式表达素数的一堆猜想,关于 Artin L-函数的 Artin 猜想,代数数n进制展开或连分数展开的 Borel 猜想,群论中的伯恩赛得猜想,等等。这些猜想难度也是无法估量的,甚至影响整个分支的进展。但是这些猜想所处的数学分支比如解析数论、代数数论、丢番图逼近、群论,即使谈不上非常成熟,但至少也是自成体系,枝繁叶茂。这些猜想虽然也是非常非常地困难,但其最终的解决也是无法脱离相关数学分支既有的数学思考范式。
然而 3n+1 猜想和上面这些数学猜想完全不一样,3n+1 猜想代表的是哪一类数学,我们完全不知道。我认为关于 3n+1 猜想的研究如果想取得重大进展,一定要彻底突破现有的数学思考范式。(不少人认为现代动力系统的不断发展有可能最终解决 3n+1 猜想,但我认为没有那么简单)
如果把上面提到的那些猜想比作数学未知海洋世界的冰山一角的话,那么 3n+1 猜想更像是从遥远而又神秘的未知世界透射过来的一缕微光。那是一个全新的数学世界,远远超越了当代所有职业数学家的数学想象力。
在我的数学职业生涯中,每隔两三年我都会抽出一段时间(短则半个月长则两三个月)来思考 3n+1 猜想。虽然每次都是无功而返,但我非常享受思考 3n+1 猜想的美好时光,那种美妙的感觉绝不亚于和一位美丽情人的幽会。










 加载中,请稍侯......
加载中,请稍侯......
网友评论